Teoretikus keret versengő személyek társadalmi attitűdjének kikövetkeztetésére, a stratégia tudománya, de legalábbis független és egymással versengő személyek kísérlete az optimális döntéshozására, ráadásul igen komoly magyar vonatkozása is van. A pszichológiától az evolúciós biológiáig, a hadviseléstől a politikáig és természetesen a gazdaságig (amelyet a versengő viselkedésformák modellezésével forradalmasított is), sok területen alkalmazzák, és a hosszú fejlődés ellenére még mindig kialakulóban lévő, fiatal tudomány. Mi az?

Igen, a játékelmélet. De miről is van szó?

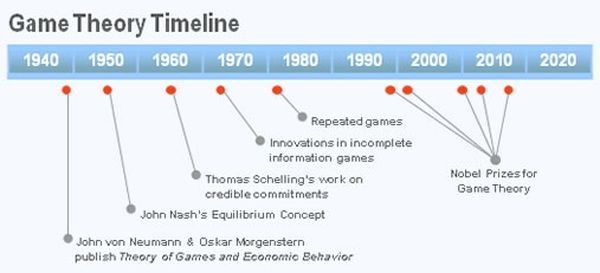
A világszerte John von Neumannként ismert Neumann János (1903-1957) és a közgazdász Oskar Morgenstern (1902-1977) az 1940-es években rakták le az alapjait. Az elmélet a racionális szereplők közötti interaktív szituációként értelmezett játékra összpontosít. Lényege, hogy az egyik játékos nyereménye a másik által megvalósított stratégiától függ.

A játék azonosítja a résztvevők identitását, preferenciáit, kivitelezhető stratégiáikat, és a stratégiáknak az eredményre, a kimenetre gyakorolt hatását. A modelltől függően számos egyéb követelmény vagy feltételezés is szükséges lehet.

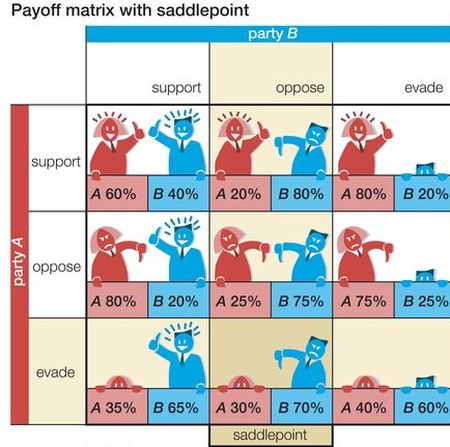
Az összes szereplő cselekvései és választásai mindegyik sorsára kihatnak. Az elmélet magától értetődőnek veszi, hogy a szereplők racionálisak, és a nyeremény maximalizálására törekednek. Bármikor, amikor két vagy több játékos olyan helyzetben találja magát, hogy az eredmény, a következmények számszerűsíthetők, az elmélet segítségével meghatározhatjuk a lehetséges kimeneteket.

A játék a döntéshozó résztvevők – a játékosok – cselekedeteitől függő körülmények sorozata. A stratégia a körülményeket figyelembe vevő cselekvési terv, a fizetség pedig az egyedi kimenetek függvénye. Az adott pillanatban rendelkezésre álló információ szintén fontos tényező, akárcsak az egyensúlyi állapot, amikor a játékosok meghozták a döntéseiket, és elérték a kimenetet.

A játékelmélet Neumann és Morgenstern melletti harmadik nagy alakjáról, a munkásságáért 1994-ben gazdasági Nobel-díjat kapott John Forbes Nash-ről (1928-2015) elnevezett Nash-egyensúly az a kimenet, amelyet ha egyszer elérnek, akkor már egyik játékos sem változtathat rajta önkényesen. Egy játékban azonban nem csak egy, hanem többfajta egyensúlyi állapot is előfordulhat. Minél komplexebb, annál inkább.

Ugyan többféle (szimmetrikus-aszimmetrikus, szimultán-szekvenciális stb.) játékelmélet van, az együttműködő-nem együttműködő a legelterjedtebb. A kooperatív azt vizsgálja, hogyan folytatnak csoportok interakciókat egymással akkor, amikor csak a végeredmény ismert. Ebben az esetben inkább játékos-koalíciókról van szó, és nem individuumokról. A nem-kooperatív játékelmélet a saját céljaik megvalósításán dolgozó racionális ágensek egymás közötti tevékenységét tanulmányozza, ezek közül a legelterjedtebbek a stratégiaiak, a legismertebb pedig a fogolydilemma.

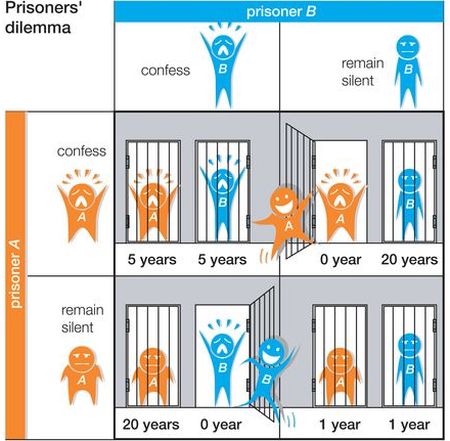
Képzeljük el, hogy ugyanazért a bűntettért fognak el két bűnözőt, de az ügyésznek nincsenek erős bizonyítékai az elitéléshez. A vallomást nem a zárkában, hanem külön-külön, más helyiségekben próbálják kiszedni belőlük. Nem kommunikálhatnak egymással. Négy kimenet lehetséges:

1. Ha mindkettő vall, öt-öt év börtönre ítélik őket.
2. Ha A vall, de B nem, A három, B kilenc évet kap.
3. Ha B vall, A viszont nem, A büntetése tíz, B-é két év.
4. Ha egyik sem vall, mindkettőt két évre ítélik el.

Legkedvezőbb, ha egyik sem vall, csakhogy nem ismerik egymás stratégiáját, úgyhogy a legvalószínűbb kimenet, hogy mindketten vallomást tesznek. A Nash-egyensúly viszont azt sugallja, hogy mindkét játékos az individuálisan legjobb, csapatként azonban a legrosszabb lépést fogja tenni.

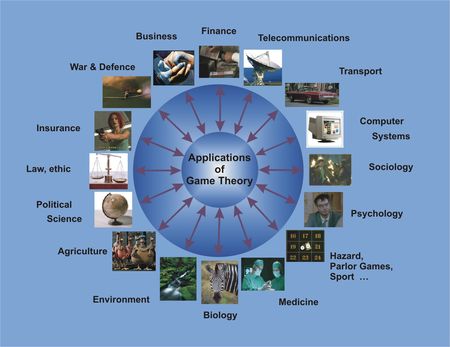
A legtöbb gazdasági modellhez hasonlóan, a játékelmélet korlátja az az alapfeltevés, hogy az emberek saját érdekeiket figyelembe vevő és a hasznot maximalizáló racionális ágensek. Valóban közösségi lények vagyunk, tudunk is együttműködni, csakhogy a társadalmi kontextustól és a résztvevők személyétől függően, egyes helyzetekben létrejöhet a Nash-egyensúly, másokban viszont nem. 

Frissítve: 2023. december 27.