Képzeljük el, hogy egy kereskedőnek, nevezzük értékesítő ügynöknek, több városon keresztül, a lehető leggyorsabban kell megtennie egy utat, mondjuk New Yorkból Bostonon, Chicagon, Kansas City-n, Denveren, Vancouveren, Seattle-n keresztül San Franciscoba. Az összes várost érintenie kell, egy adott városban azonban csak egyszer járhat.

Melyik a legrövidebb útvonal? – hangzik a kérdés, ami egyben egy könnyen érthető, ám annál nehezebben megoldható matematikai-logikai játék is: az utazó ügynök problémája.

Különböző tudományokban merül fel, a megoldásokat számos területen igyekeznek alkalmazni. A mesterségesintelligencia-kutatásban szintén népszerű feladat, gyakran állnak elő izgalmas javaslatokkal, például genetikus algoritmusokkal vagy rajintelligenciával többször találtak rá hatékony megoldást. 

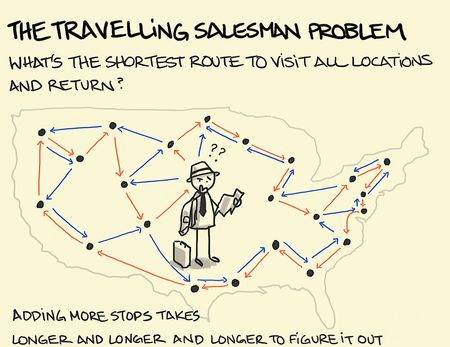
A genetikus algoritmusokon alapuló opcióban a változók egy bájtnyi (nyolc bit) egységekben tárolódnak, s mivel nullák és egyek lehetnek, értékük nulla és 255 [2 a nyolcadikon (256) mínusz egy] közötti. Mindkét irányban (x, y) nullától 255-ig terjedő négyszögletes területet vázol fel, 256-szor 256 egységgel. Tetszőlegesen kiválasztunk, és benépesítünk 256 párt, melyek száz karakterláncot formálnak (a nulla és 255 közötti indexek listájából). Egy láncon belüli valamennyi gén egyedi; szorosan kapcsolódik az előző generációhoz. Evolúciós folyamatokon (öröklődésen, mutáción) megy keresztül. Újabb láncok jönnek létre, a korábbiak pedig elpusztulnak.

A szülők kiválasztását, a következő generációban való túlélést rulett-kerék szelekciós algoritmus dönti el. Az alkalmasabb láncoknak törvényszerűen nagyobb az esélye. Míg a mutáció egyszerűen megy végbe, s igen ritkán (egyszázalékos gyakorisággal) alkalmazzák, az esetek hetven százalékában bekövetkező kereszteződésnél gondosan meg kell határozni, mitől erősebb egy-egy lánc alkalmazkodóképessége. Viszont, ha nincs kereszteződés, az utódok a szülők módosítás nélküli másolatai lesznek.

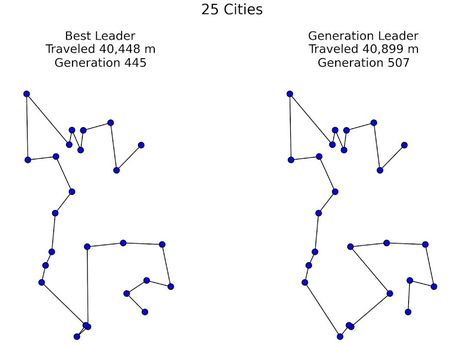
Az algoritmusokat tesztelve a szemlélődő meggyőződhet, miként fejlődnek merevebbekből véletlenszerűbbekké. A populáció globális alkalmazkodóképessége minden egyes iteráció után nő, és végül megkapjuk az egyetlen legrövidebb útvonalat, amiről fogalmunk sem volt az elején.

A genetikus algoritmusok mellett, kutatók arra is rájöttek, hogy a hangyák azon képessége, hogy a lehetséges útvonalak közül (feromon-lerakódás alapján) rátalálnak a legrövidebbre, az utazó ügynök problémájára is adhat működő megoldást.

A mesterséges hangyakolónia-rendszerekből kiindulva, az utazóügynök-probléma (TSP) gráfján a hangyák városról városra mozgó ágensek. Véletlenszerűen indulnak el, virtuális feromont hagyva maguk után. Valószínűség és az információként szolgáló, korábban lerakott feromon alapján döntenek. Miután befejeztek egy-egy utat, a gráf élein hagynak nyomot, a rövidebb út mentén természetesen többet. Végül – azt az élt választva, ahol a legtöbb a speciális illatanyag – kialakul az optimális útvonal.

A folyamat sokszori lefuttatását követően egyértelmű, hogy a felhalmozott feromon mennyisége befolyásolja a hangyatársakat. A nyomok lokálisan és globálisan is változnak. A globális frissítés a rövidebb út menti él jutalmazását célozza. A lokális ellentétes előjelű; rendeltetése nyomeltüntetés, az erősebb koncentrációk elkerülése. A hangyák vagy a bejáratott ösvényen haladnak, vagy újabb megoldások, új típusú felfedező stratégiák után kutatnak.

 A számítógépes szimuláció bebizonyította, hogy a mesterséges kolóniák a TSP szimmetrikus és aszimmetrikus példáira egyaránt találnak megoldást.

A mesterséges állatkák természetben élő társaikra nem jellemző, viszont a TSP-alkalmazások során hasznos adottságokkal is rendelkeznek. Meg tudják határozni a városok távolságát, minden út előtt kiürítendő munkamemóriájuk van, amely arra szolgál, hogy emlékezetben tartsák, mely városokban jártak már.

Frissítve: 2023. december 26.