A legendás városépítő játékban, a Sim City-ben komplett mesterséges városokat, társadalmakat dolgozhattunk ki néhány órányi játékkal. A városépítő játékokhoz hasonlóan az egyre nagyobb skálájú számítógépes szimulációk is lehetővé teszik társadalmi jelenségek, folyamatok, sőt, egész társadalmak pontosabb modellezését, hipotetikus modellek összekombinálását valódi adatokkal.
Az adatrobbanás, a big data és a mesterségesintelligencia-megoldások gyors fejlődése rengeteget segít az elemzésekben fontos szerepet játszó, alulról felfelé (bottom-up) szerveződő, ágensalapú mesterséges társadalmak szimulálásában. Ezek a szimulációk lehetőséget adnak arra is, hogy tanulmányozzuk, hogyan tegyük jobb hellyé a világot.
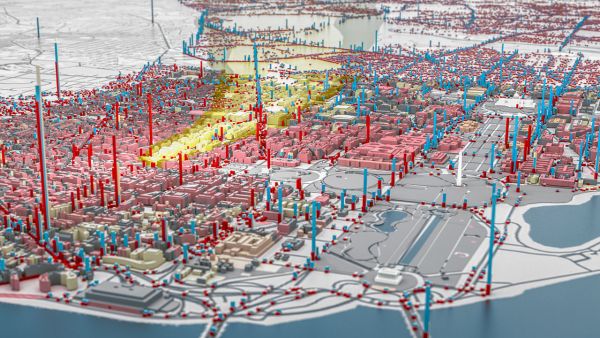
A mesterséges társadalom koncepciója olyan számítástudományi módszerekhez, technikákhoz kapcsolódik, mint az evolúcióalapú programozás, a multi-ágens és a komplex rendszerek, vagy az ágenskutatásból jól ismert emergencia. Az elképzelés elég egyszerű, a kivitelezés annál bonyolultabb. Komplex matematikai modellek régóta léteznek, a jelenleg elérhető számítógépes kapacitások nélkül viszont csak csúcslaborokban lehetett hatékony szimulációkat futtatni.
Az emberi interakcióra vonatkozó, mindössze néhány szabály felállításával bonyolult önszerveződő rendszerekhez hasonló „társadalmak” hozhatók létre. Véletlen események bevezetésével különös, nem teljesen véletlen, előre nem definiálható jelenségek figyelhetők meg. A modellek a jövő pontos előrejelezhetőségének bizonyítása helyett inkább arra hívják fel a figyelmet, hogy a társadalmi, politikai, gazdasági stb. élet mely pontjain számíthatunk meglepetésekre, nem várt jelenségekre.
Ráadásul ugyanaz a modell több, nem egyszer gyökeresen eltérő megoldást eredményezhet. A módszerrel egyébként nemcsak a jövő vagy a jelen társadalmi trendjei, hanem a múlt, például – ismert (földrajzi, éghajlati, néprajzi stb.) adatok alapján modellezett folyamatokra támaszkodva – megoldatlan történelmi jelenségek, rejtélyek is vizsgálhatók, és hamar kiderül, hogy a tegnapot ugyanolyan nehéz előrejelezni, mint a holnapot.
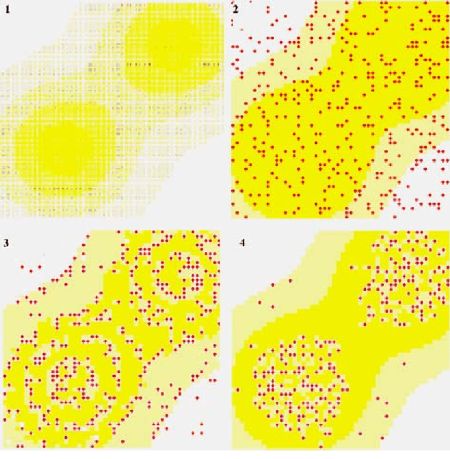
A mesterséges társadalmak és az ágensalapú modellezés Neumann János sejtautomatájáig, az önmaga reprodukálására képes gépek elméletéig vezethetők vissza. Stanislaw M. Ulam az 1940-es években, Los Alamosban különböző számítógépes mintajátékokat talált ki. Meghatározott szabályok alapján a számítógép állandóan átalakuló, „szinte élő” mintázatokat, geometriai formákat nyomtatott ki. A sejtekből összeálló alakzatok gyakran egymást megsemmisítve küzdöttek az élettérért. Egy-egy sejt „élete” a szomszédoktól függött.
Ulam javaslatára Neumann János a mintajátékokat végtelenített sakktáblára alkalmazta. A sejtstruktúrára (s így egy – az absztrakt világot működtető – leegyszerűsített fizikára) azért volt szüksége, mert nélküle rendkívül nagy, szinte mérhetetlen mennyiségű kapcsolat jönne létre az összetevők között. Végül sikerült megvalósítania az elméleti modellt, és bebizonyította, hogy megfelelő átmeneti függvénnyel a sejtautomata univerzális és önreprodukáló.
Neumann munkájából kiindulva az adaptáció és az optimalizálás problémájára alkalmazva, a „genetikus algoritmusok atyjaként” emlegetett John Holland az 1970-es években általános sejtautomata-szimuláló programot fejlesztett.
A bonyolultabb és izgalmasabb kétdimenziós automatákat vizsgálva, John Horton Conway brit matematikus az 1970-es évek elején dolgozta ki az Életjátékot, a legismertebb (négyzethálós) sejtautomata modellt. Két állapotot, négy egyszerű szabályt használt, sejtenként nyolc szomszédos cellával, cellánként maximum egy sejttel: ha egy élő sejtnek kettőnél kevesebb szomszédja van, akkor meghal; ha háromnál több szomszédja van, akkor is meghal; ha egy halott sejtnek (üres cellának) pontosan három szomszédja van, akkor életre kel; különben, az összes többi sejt eredeti állapotában marad.
A gyorsan, számítógéppel másodpercenkénti több generációs sebességgel pergő játék során különös alakzatok keletkeznek, csoportok bukkannak elő, tűnnek el, aszimmetrikus formák szimmetrikusokká fejlődnek – pontosan úgy, mint az életben.
Ágensalapú megoldást először (az 1980-as években) Craig Reynolds használt társadalmi modellként. Élő biológiai ágenseket a mesterséges életként ismert módszerrel próbált modellezni.
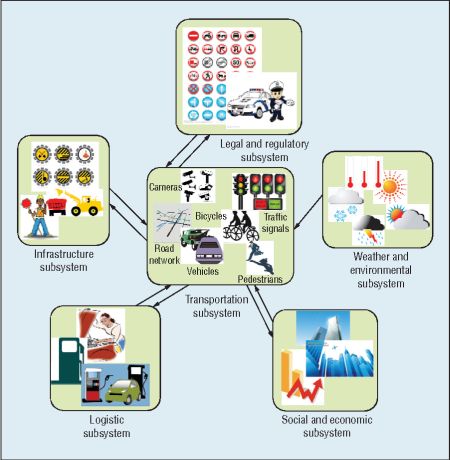
Az eljárást hamarosan társadalmi rendszerekre kezdték alkalmazni, innen származik a mai szociológiában széles körben elfogadott, interdiszciplináris „mesterséges társadalmak” kifejezés.
Frissítve: 2025. június 16.